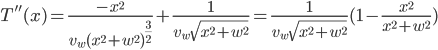This is a classic introductory calculus problem, with a Minecraft theme. This particular variation is inspired by example 4 in section 4.5 of Stewart's calculus.
I'll set the scene: You're weaponless. You have half a heart and you're being chased by a skeleton archer. There's a river between you and your cabin. You need to get to your cabin as quickly as possible!

In more "mathy" terms, you want to get from  to
to  . There are three main ways you can do this:
. There are three main ways you can do this:
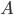 to
to 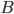 directly, diagonally across the river
directly, diagonally across the river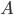 to
to 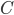 and then
and then 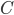 to
to 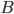
- At slight angle from
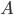 to
to 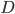 and then
and then 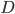 to
to 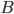
We know that swimming is slower than running, so option 1 isn't the best. Option 2 involves the smallest time in the water, but also the longest distance traveled.
Option 3 is somewhere in between - you spend a bit more time in the water, but the total distance is decreased. The travel time in this case depends on where exactly point 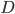 is. To find the optimal path, we must find the position of
is. To find the optimal path, we must find the position of 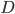 which minimizes the travel time. This sounds like calculus!
which minimizes the travel time. This sounds like calculus!
Let 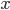 be the distance between points
be the distance between points 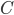 and
and 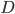 . In math terms,
. In math terms, 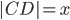 .
.
We first need an expression for the total time traveled in terms of 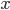 . The basic equation for time traveled at constant speed is
. The basic equation for time traveled at constant speed is
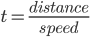 .
.
The first part of the trip is in the water where we travel from 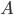 to
to 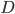 . We can use Pythagorean's theorem to get this distance as
. We can use Pythagorean's theorem to get this distance as 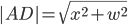 . Assuming that we can travel at a speed of
. Assuming that we can travel at a speed of 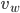 in the water, the time for this part is
in the water, the time for this part is
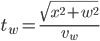 .
.
The land part of the trip involves traveling what's left over of 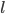 after having already traveled
after having already traveled 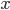 , so
, so 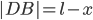 . Traveling at
. Traveling at 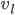 on land, the time for this part of the trip is
on land, the time for this part of the trip is
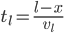 .
.
The total trip time, 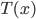 , is just the sum of these two.
, is just the sum of these two.
 (1)
(1)
To optimize this function with respect to  , we need to find where it is stationary and then verify that this point is a minimum. This means we want to find a place where the function isn't changing with small changes in
, we need to find where it is stationary and then verify that this point is a minimum. This means we want to find a place where the function isn't changing with small changes in  . In other words, we want to find a spot where the derivative is zero.
. In other words, we want to find a spot where the derivative is zero.
Taking the derivative gives:
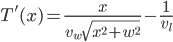
Setting this equal to zero, we can solve for 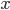 :
:
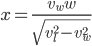 (2)
(2)
Let's plug in some numbers! In Minecraft, you can swim at about 2.2 m/s and sprint at 5.6 m/s. Let's take the river width 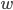 to be 7 blocks (1 block = 1 meter). Plugging in, we find that
to be 7 blocks (1 block = 1 meter). Plugging in, we find that 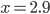 . At this point, though, we can't tell if this is a maximum or a minimum. One way to find out is to examine the curvature of the function at this point by using the 2nd derivative:
. At this point, though, we can't tell if this is a maximum or a minimum. One way to find out is to examine the curvature of the function at this point by using the 2nd derivative:
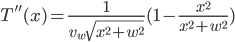
Plugging in 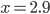 , we see that
, we see that 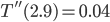 which, being positive, means that
which, being positive, means that 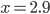 is a minimum point for
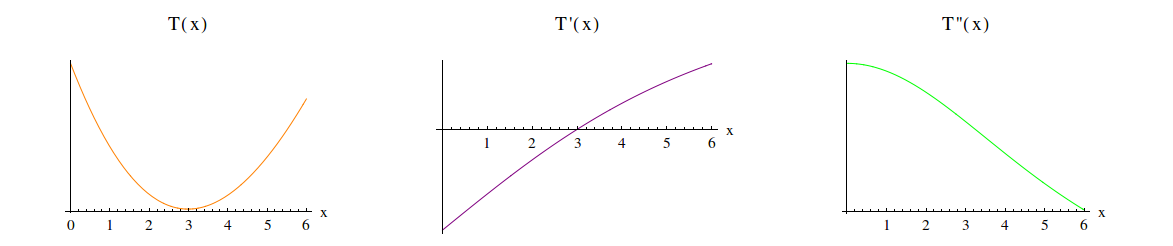
is a minimum point for 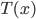 . Visually:
. Visually:
So if you want to get to your cabin as quickly as possible, the fastest route is to swim across the river to a point 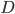 that is 2.9 meters from point
that is 2.9 meters from point 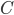 and then run the rest of the way.
and then run the rest of the way.
This is actually a general problem. Try replacing the speeds I used with speeds for soul sand, crouching and walking, a boat, etc. and see what happens! Particularly, what happens to (2) if you can travel more quickly in the water than on land?
Scratch Work
Finding 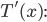 First, rewrite the square root as a power,
First, rewrite the square root as a power, 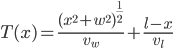
Differentiating, using the chain rule on the first term, 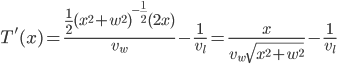
Finding 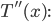 Starting with
Starting with 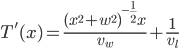 , we differentiate with respect to x. Note that the derivative of
, we differentiate with respect to x. Note that the derivative of 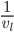 with respect to
with respect to 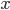 is 0, so we only have to deal with the first term. Using the product rule and chain rule:
is 0, so we only have to deal with the first term. Using the product rule and chain rule:
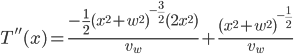
Cleaning up with some algebra: