A very common statistic in video games is the kills-to-deaths ratio (KD), which is computed as the number kills divided by the number deaths you've achieved in the game. The KD is very popular in first person shooters, but can be found in most any place where there's player vs. player combat. Your KD can be interpreted as the number of kills you tend to get for each death you accumulate (environmental or otherwise). As you play your game of choice you (hopefully) get better with time, which is reflected in your increasing KD. However, you may have noticed that the rate at which your KD increases slows down over time (KD lag). Let’s see why.
First let’s figure out how much your KD increases when adding 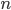 kills.
kills.
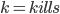
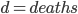
Let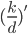 be your new KD after adding
be your new KD after adding 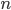 kills to your old KD.
kills to your old KD.
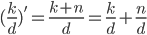
Notice that if we subtract 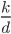 from both sides we end up with
from both sides we end up with
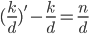 (eq. 1)
(eq. 1)
The quantity on the left is simply the difference between the old KD and the new KD. Essentially, it’s the how much your KD changes if you add 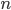 kills. Let's call that
kills. Let's call that 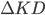
So, a change in KD from adding 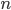 kills is
kills is
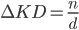
This is interesting because the change is completely independent of your total kills, and only depends on your total deaths.* The 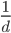 dependence is one of the reasons why your KD seems to slowly creep along as you play more (and rack up more deaths). Of course, there are other factors too such as the fact that people don't actually get better at the game at a constant rate for as long as they play, but that's the topic of another discussion.
dependence is one of the reasons why your KD seems to slowly creep along as you play more (and rack up more deaths). Of course, there are other factors too such as the fact that people don't actually get better at the game at a constant rate for as long as they play, but that's the topic of another discussion.
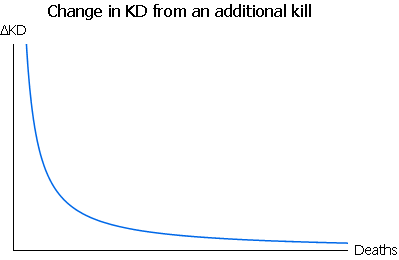
Kind of scary, isn't it! So, the TL;DR is:
The more deaths you have, the less you gain in KD from killing someone.
You can use this information to easily figure out how many kills you need to get (without dying!) to reach a new target KD. Simply solve eq. 1 for 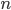 :
:
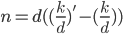
Or, to write it in a way that's easier to read/ use, the number of kills you need (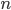 ) to reach a target KD is:
) to reach a target KD is:
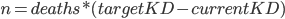
Again, notice the dependency on deaths. As your deaths go up, so do the necessary number of kills needed to reach a given target KD.
*You may notice that if the d’s are all the same in eq. 1, you can cancel them out. But this just leaves us with 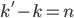 , telling us that the difference between the old kills and new kills is the number of kills you added, which is sort of obvious and not interesting. So leave the d's in there for now!
, telling us that the difference between the old kills and new kills is the number of kills you added, which is sort of obvious and not interesting. So leave the d's in there for now!