GG! Good game! This little web app was my Sunday project. It collects data and computes some basic statistics for Minecraft player-vs.-player minigame matches on the Overcast Network servers. It's still very much a work in progress, but check it out! Also, see the project on GitHub.
minecraft
There are 4 posts tagged minecraft.
Minecraft Calculus: River Crossing Escape
This is a classic introductory calculus problem, with a Minecraft theme. This particular variation is inspired by example 4 in section 4.5 of Stewart's calculus.
I'll set the scene: You're weaponless. You have half a heart and you're being chased by a skeleton archer. There's a river between you and your cabin. You need to get to your cabin as quickly as possible!

In more "mathy" terms, you want to get from 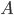 to
to 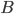 . There are three main ways you can do this:
. There are three main ways you can do this:
 to
to 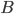 directly, diagonally across the river
directly, diagonally across the river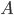 to
to 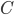 and then
and then 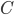 to
to 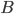
- At slight angle from
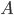 to
to 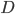 and then
and then 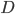 to
to 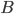
We know that swimming is slower than running, so option 1 isn't the best. Option 2 involves the smallest time in the water, but also the longest distance traveled.
Option 3 is somewhere in between - you spend a bit more time in the water, but the total distance is decreased. The travel time in this case depends on where exactly point 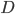 is. To find the optimal path, we must find the position of
is. To find the optimal path, we must find the position of 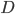 which minimizes the travel time. This sounds like calculus!
which minimizes the travel time. This sounds like calculus!
Let 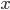 be the distance between points
be the distance between points 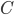 and
and 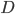 . In math terms,
. In math terms, 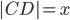 .
.
We first need an expression for the total time traveled in terms of 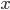 . The basic equation for time traveled at constant speed is
. The basic equation for time traveled at constant speed is
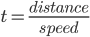 .
.
The first part of the trip is in the water where we travel from 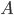 to
to 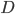 . We can use Pythagorean's theorem to get this distance as
. We can use Pythagorean's theorem to get this distance as 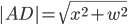 . Assuming that we can travel at a speed of
. Assuming that we can travel at a speed of 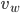 in the water, the time for this part is
in the water, the time for this part is
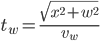 .
.
The land part of the trip involves traveling what's left over of 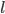 after having already traveled
after having already traveled 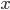 , so
, so 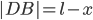 . Traveling at
. Traveling at 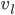 on land, the time for this part of the trip is
on land, the time for this part of the trip is
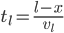 .
.
The total trip time, 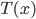 , is just the sum of these two.
, is just the sum of these two.
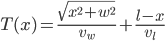 (1)
(1)
To optimize this function with respect to 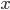 , we need to find where it is stationary and then verify that this point is a minimum. This means we want to find a place where the function isn't changing with small changes in
, we need to find where it is stationary and then verify that this point is a minimum. This means we want to find a place where the function isn't changing with small changes in 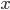 . In other words, we want to find a spot where the derivative is zero.
. In other words, we want to find a spot where the derivative is zero.
Taking the derivative gives:
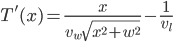
Setting this equal to zero, we can solve for 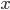 :
:
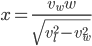 (2)
(2)
Let's plug in some numbers! In Minecraft, you can swim at about 2.2 m/s and sprint at 5.6 m/s. Let's take the river width 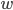 to be 7 blocks (1 block = 1 meter). Plugging in, we find that
to be 7 blocks (1 block = 1 meter). Plugging in, we find that 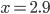 . At this point, though, we can't tell if this is a maximum or a minimum. One way to find out is to examine the curvature of the function at this point by using the 2nd derivative:
. At this point, though, we can't tell if this is a maximum or a minimum. One way to find out is to examine the curvature of the function at this point by using the 2nd derivative:
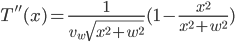
Plugging in 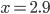 , we see that
, we see that 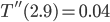 which, being positive, means that
which, being positive, means that 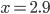 is a minimum point for
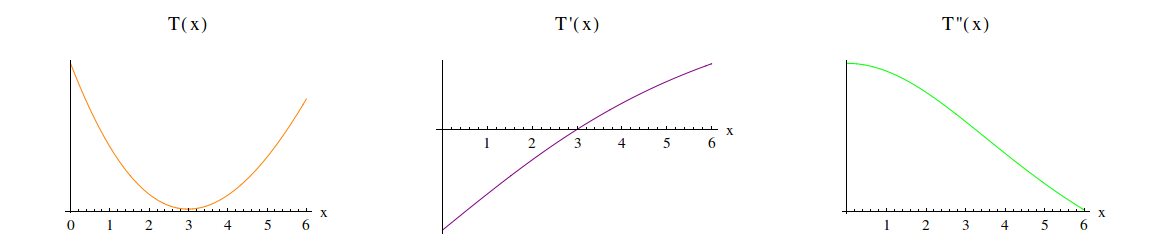
is a minimum point for 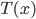 . Visually:
. Visually:
So if you want to get to your cabin as quickly as possible, the fastest route is to swim across the river to a point 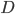 that is 2.9 meters from point
that is 2.9 meters from point 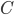 and then run the rest of the way.
and then run the rest of the way.
This is actually a general problem. Try replacing the speeds I used with speeds for soul sand, crouching and walking, a boat, etc. and see what happens! Particularly, what happens to (2) if you can travel more quickly in the water than on land?
Scratch Work
Finding 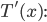 First, rewrite the square root as a power,
First, rewrite the square root as a power, 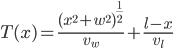
Differentiating, using the chain rule on the first term, 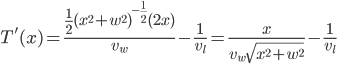
Finding 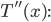 Starting with
Starting with 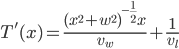 , we differentiate with respect to x. Note that the derivative of
, we differentiate with respect to x. Note that the derivative of 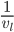 with respect to
with respect to 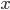 is 0, so we only have to deal with the first term. Using the product rule and chain rule:
is 0, so we only have to deal with the first term. Using the product rule and chain rule:
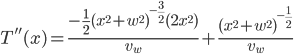
Cleaning up with some algebra:
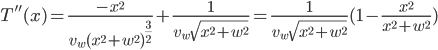
Project Ares Beta Tournament: Predictions vs. Outcome
Update and Reflection (October 2015):
WOW! This was almost two years ago. It's pretty funny looking back at these old blog posts. This is probably the first actual "data science" project I ever worked on, and now I get paid to do silly things like this which is pretty cool. So yeah, if you're looking to get into software or data science, you have to find random little projects to work through. It might be embarrassing to look back, but in the end if you're learning stuff that's all that matters. Thanks for letting me scrape your website for all of these years, guys! Cheers!
I've added some additional comments at the bottom of the article.
Original Article:
Project Ares held their first full tournament yesterday. This included 16 teams playing a variety of maps, and it lasted a whopping 8 hours!
Anyway, I thought it would be fun to compare all of the teams competing using some of the statistical data available on the Project Ares site to see how well of a performance predictor it is. There are three main statistics: KD, KK and OD. They are defined as follows:
- KD = kills/deaths
- KK = kills/times killed by another player
- OD = objectives completed / deaths
KD and KK are directly related to fighting skills, where as OD has more to do with completing objectives (capturing wools and leaking cores).
I compared teams by taking the average of each of these three quantities for each team.
Results
Predicted Bracket
Actual Bracket (link now broken, October 2015)
The KD and KK ratios give identical predictions. The OD ratio, on the other hand, is a very poor indicator of performance.
Using the team's average KD (or KK) alone, I was able to predict 12 out of 15 matches (accuracy of 80%), including the semifinals and tournament winner and most match outcomes (there were only three upsets: two pictured and one when YoloSwag beat Impact in Round II). Of course, minecraft gameplay is complex and the three statistics alone do not represent all of the skills required to win a match, but it does seem to be a pretty strong indicator of overall performance.
Looking at the numbers, it is quite clear that the winning team, Badlion, is totally stacked. Their average KD was 3 times that of the overall average.
Other Stuff
I decided this would be a neat idea late last night after the tourney ended, so the way I built the bracket is a bit of a mess (a combination of an extremely inefficient Mathematica script and google docs). But, I plan on playing with this more and automating it better for future use.
More Update Stuff (Still October 2015)
So what's changed? An accuracy of 80% using only player's KD ratios is pretty crazy. In fact, since the first tournament, it is no longer possible to make such a "good" prediction. I think there are two reasons why KD has lost its predictive power:
- Since the first tournament, players have begun boosting their stats to get on teams. This includes playing differently than you would in a tournament (e.g. cautiously farming), making them less reflective of actual ability and more of patience.
- People strat the hell out of maps now. Players knew maps during the first tournament, but now teams are in general much more organized and practice a lot more, trying to exploit every little opportunity each map has to offer.
I think point 1 isn't as important, because most good players know that stats aren't necessarily an indicator of skill level. At the end of the day everyone does a little sword fighting, but map-specific knowledge and team organization still plays an enormous role in winning matches.
Now that Overcast Network (which was named "Project Ares" when this post was originally written) has introduced a more sophisticated ranking system, I'm looking forward to squeezing some information out of that data next time around.
Budder Mod
Okay, this is probably only amusing to those who play on some awesome minecraft server (it's kind of an inside joke), but I thought I'd post it here anyway. I'm relatively new to the minecraft plugin scene (I have no idea what I'm doing), so this seemed like an easy project for me to get familiar with the very basics of the bukkit server API.
It's a very simple mod that is as useless as it is amusing (to me at least - if you don't find it amusing, you probably still won't find it useful).
Upon death by a gold sword, the plugin modifies the death message displayed:




and shoots some gold fireworks in the air:


My trolling turned out to be amusing to some, and too subtle for others (which I guess is good trolling?).