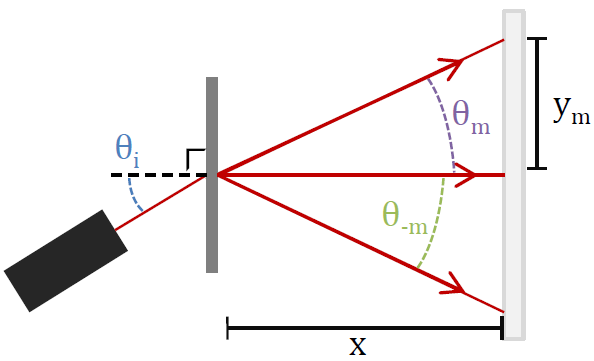
A laser beam passing through a transmission diffraction grating straight on gives the standard diffraction pattern we all know and love.  It's a bit more interesting, though, if the beam hits the grating at an angle:

figure 1

Most intro optics books cover this situation, and the result is (equation 1):

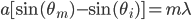
where 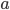is the grating spacing, 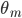is the angle of the mth maxima,  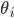is the incident angle, 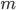is the maxima order, and  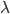is the wavelength. We can rewrite this (homework) in a more useful way as (equation 2):

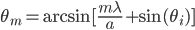
A similar, but slightly more complicated situation happens when you rotate the grating instead of the lazer: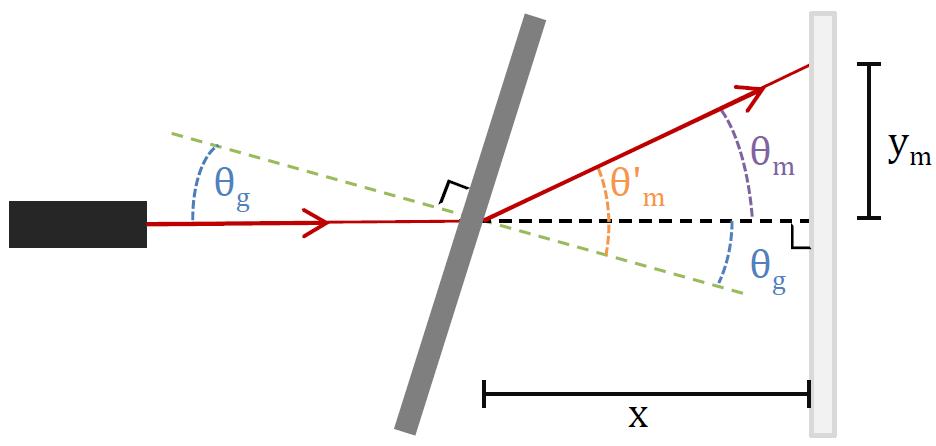

figure 2

With a rotated grating (figure 2), the laser is still hitting the grating at an angle as it is in figure 1.  So, starting with equation 2 and using some geometry we get the angles that satisfy the maxima condition:

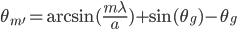
This seemed liked a fun thing to model in Mathematica, especially since I had never played with any of the graphics features before.

You can view the source here.

You need Wolfram's CDF player, but it's totally worth because then you can look through all of the awesome demonstrations they have online.