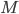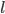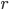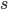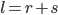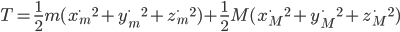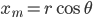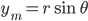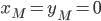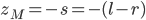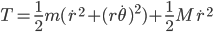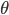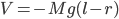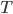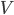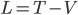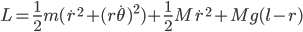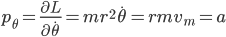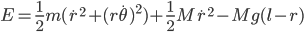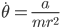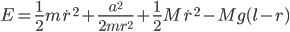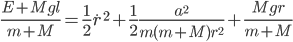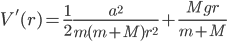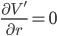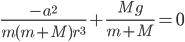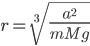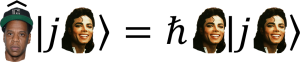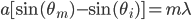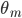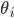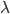physics

There are 6 posts filed in physics.

Minecraft Physics: Steve in Drag

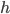An object falling under constant acceleration travels a distance in an amount of time 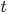given by

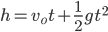
where 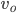is the object's starting velocity.  For an object dropped from rest, 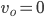.  Plugging that in and solving for , we find

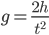   (1)

Using this equation, we can approximate the acceleration due to gravity in Minecraft by timing how long it takes something to fall some distance.  This model assumes constant acceleration, which means it ignores things like drag forces from air resistance.  It turns out, Minecraft actually does have air resistance, but we will get there a bit later.

Youtuber nopefully used the above approximation to determine the gravitational acceleration of sand blocks (further analyzed here).  Since then, though, the addition of command blocks and scoreboards provide a simple way to time things in game, so that's the approach I'll take.

Experiment

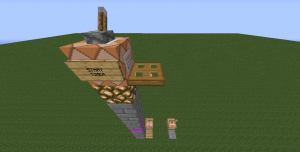
The dropper platform

Figure 1: The dropper platform.

Timer stop and reset

Figure 2: Timer stop and reset. The clock circuit is in the background.

The experiment is simple: jump off of stuff, time it with command blocks, and plug the result in the above equation (1) to figure out the gravitational acceleration of a player.  For timing, I used Sethbling's stopwatch design.  The timer-starting command block (figure 1) is activated by a lever which also triggers a trapdoor, causing you to fall onto a pressure plate below, stopping the timer (figure 2).

I repeated this experiment five times at three different heights.  The data is in the table below (remember, a Minecraft block is 1 meter on each side):

Table 1: Results
Height (m) Average Fall Time (s) Acceleration (m/s2)
10 0.94 22.63
20 1.34 22.28
40 1.88 22.63

So using model (1), Minecraft's gravitational acceleration is around 23 m/s2.  But as I mentioned above, we're neglecting air resistance.  There isn't an easy way to experimentally measure the air resistance, but luckily a video game provides us with something that nature does not: the source code.  So let's cheat a little bit and take a look under the hood.

Cheating

In the EntityLivingBase class, there's a method named moveEntityWithHeading that is called 20 times per second (each "tick"), updating the entity's velocity.  If there isn't a block under the living entity (in other words, it's falling), the downward velocity is increased by 0.08 and decreased by 2% each tick.  This means there's a constant acceleration component that is 0.08 blocks/tick2 = 32 m/s2 and a drag force that is directly proportional to the velocity.  32 m/s2 is a lot different than our measured 23 m/s2, so clearly the drag force is not something that can be ignored.  Also, 32m/s2 is over 3 times greater than the gravity on Earth!  (An inventory of cobble is seriously heavy.)

On Earth, the gravitational acceleration is about 9.8m/s2 near the surface, and is the same for all objects regardless of how much they weigh.  This isn't the case in Minecraft, as you can see in the more detailed table on Minecraft wiki.  The "drag" contribution is also different for different entities (which is slightly more realistic since air resistance depends on the size and shape of the object).

 

Fluid Dynamics

The existence of a non-negligible drag force complicates the task of experimentally determining Minecraft's gravitational acceleration.  But it also means that we have a more fun differential equation to play with!  We can start out by writing down the equations of motion for the object falling.  From the source code, we know that the drag force is proportional to the velocity, so we can use a linear drag model for the forces:

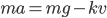
where 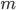is the object's mass, 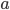is the total acceleration, 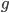is the acceleration due to gravity, 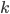is some sort of drag coefficient and 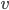is the object's velocity.  Remembering from physics class that acceleration is the first derivative of velocity with respect to time (denoted 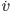), we can substitute 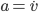.  Doing that and diving both sides by 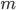gives us an equation for the total acceleration:

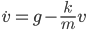
The value of is what's in the "Drag" column in the Minecraft wiki table.  Solving for the velocity as a function of time, we find

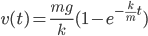   (2)

We can take some values of and 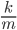from the table and graph the velocity (equation 2) of each of the different entities as they fall:

The velocity increases for a bit, but the rate at which it increases (the acceleration) slows with time until the entity travels at a constant velocity.  This is called terminal velocity, and it's reached when the gravitational force and the force due to air resistance balance out.  You can see that a falling player can catch up to most other entities, except for fired arrows.*

You can see the raw data in a Google spreadsheet here.  I encourage you to try out this set up and Minecraft physics experiments.  Please share your findings!

 

*So if, for example, you're engaging in a PvP fight on Overcast Network and someone tries to jump out of the world to deny you a kill, look over the edge and shoot!  Your arrow has a chance of catching up to them.

From the notes: Two masses on a string going through a hole

Two masses on a string going through a hole.  Yeah, that's the stuff we learn about in physics class.  Anyway, this is the first in a (possibly) series of posts where I work out some problem from my lecture notes or homework.  The reason for doing this is because 1) there's a (small) chance it will be useful or interesting to someone else, and 2) the drawn out process of typing this up and thinking about how to explain it helps me study.

Figure 1, two masses on a string going through a hole.

 

Consider two masses connected by a string (figure 1).  The ideal string passes through a hole in a plate which is parallel to the x-y plane.  One mass, is sitting on the plate and is free to rotate about the hole with no friction.  The second mass, , is hanging below the plate and moves only in the vertical z direction under the influence of gravity.   The total length of the string is and we define and to be the distances between the hole and and , respectively, so that .

We can use Lagrangian mechanics to explore the system.  In Cartesian coordinates, the total kinetic energy is the sum of the kinetic energy of each mass:

     (1)

where we've used the dot notation for time derivatives.

Considering that is only rotating about the axis and is moving only vertically, it makes sense to consider switching to a more reasonable coordinate system.  We can transform to cylindrical coordinates with:

Taking derivatives of these with respect to time and inserting them into (1), we can rewrite the kinetic energy in cylindrical coordinates as

where and are now the generalized coordinates of the system.  The potential energy depends only on the height of since is confined to sit on the plate, so

With and we can write the Lagrangian :

We see that does not appear in the Lagrangian, which means that the generalized momentum corresponding to is a conserved quantity:

     (2)

can be identified as the angular momentum of mass .

We can also look at the total energy :

     (3)

From (2) we see that .  Substituting this in (3) gives

We can separate the constants on the left hand side and use the remaining terms to define an effective potential :

Imagine is rotating about the hole.  This means there will be some centripetal (or centrifugal, depending on your reference system) acceleration which will pull the hanging mass up.  We want to find such that the force is an extremum.  In other words:

Setting the derivative equal to zero gives

And solving for :

which gives the radius of "orbit" of mass about the hole for a given angular momentum such that remains suspended in the air.

 

The physics of Jake Brown's ollie 720

I'm a couple weeks late on this, but recently Jake Brown landed the first ever ollie 720.  To put that in layman's terms, he did two full rotations without holding the board on his feet with his hands.  Check it out:

 

 

So this seems crazy.  How did he do that?  How did he keep the board on his feet?  Magnets?  It turns out, it's actually very simple physics:

The Conservation of Energy

 

That's it!  Jake Brown doesn't really have to do anything because the conservation of energy won't be violated (it's a law!).  So yeah, thanks physics!  Skateboarding is so easy.

 

 

Popularizing Science One Operator at a Time

One thing I'm very interested in is the popularization of science and other STEM related fields.  I feel that it's very important to maintain a society that is both scientifically literate and scientifically enthusiastic.

This has motivated me to purpose a new notation for the total angular momentum operator in quantum mechanics that will be more appealing to the general public and more specifically the "cool youth" of today:

 

totalAngMom_newNotation

 

It's like flipping through a celebrity gossip magazine while you compute matrix elements!

Fun with Diffraction Gratings

A laser beam passing through a transmission diffraction grating straight on gives the standard diffraction pattern we all know and love.  It's a bit more interesting, though, if the beam hits the grating at an angle:

grating1

figure 1

Most intro optics books cover this situation, and the result is (equation 1):

where is the grating spacing, is the angle of the mth maxima,  is the incident angle, is the maxima order, and  is the wavelength. We can rewrite this (homework) in a more useful way as (equation 2):

A similar, but slightly more complicated situation happens when you rotate the grating instead of the lazer:grating

figure 2

With a rotated grating (figure 2), the laser is still hitting the grating at an angle as it is in figure 1.  So, starting with equation 2 and using some geometry we get the angles that satisfy the maxima condition:

This seemed liked a fun thing to model in Mathematica, especially since I had never played with any of the graphics features before.



You can view the source here.

You need Wolfram's CDF player, but it's totally worth because then you can look through all of the awesome demonstrations they have online.