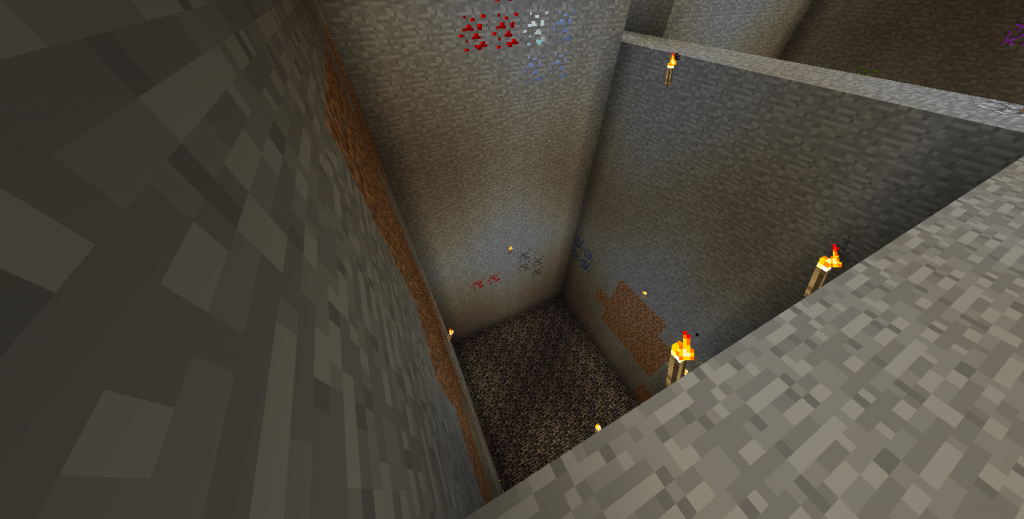
I just recently began playing with ComputerCraft, which is a very cool Minecraft mod that adds programmable computers.   There are also turtles, which are basically computers that can carry out tasks like mining, digging, attacking, etc.  Turtles are fully programmable using Lua and various APIs.  You can do lots of amazing things with turtles.

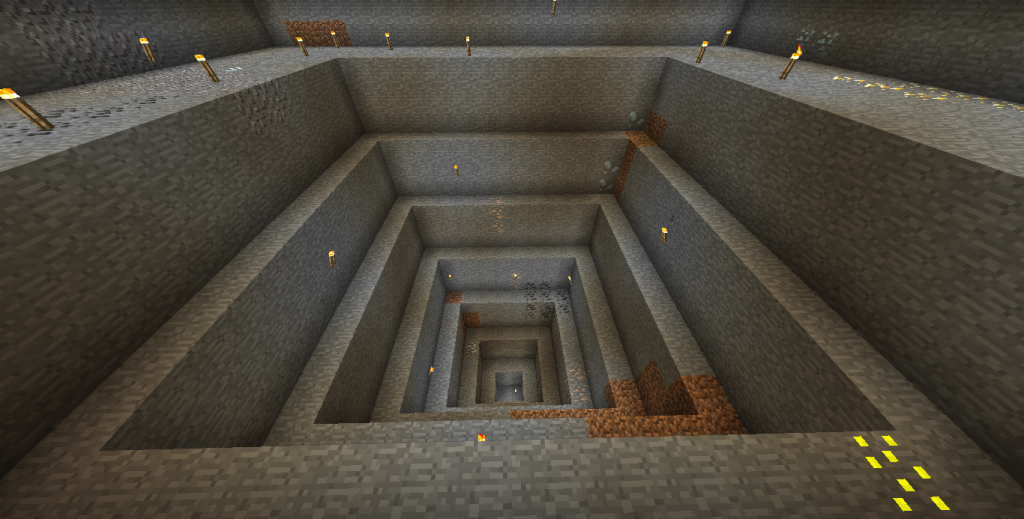
This is not something amazing, but just a simple modification I made to the turtle's excavate program that allows you to dig stepped quarries giving easier retrieval of the ores around the edges:

9x9 excavate:

14x14x3 quarry:

 Source. You can copy this script directly to your turtle using the turtle's pastebin program.

To dig a quarry, you specify the diameter 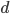and the number of blocks to dig down at each diameter, .

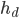It's a fun exercise to work out some of the properties of the resulting quarries.  Given a 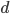and 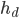, you can dig a quarry that is 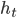blocks deep, where 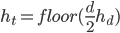if 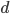is even and 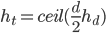if 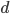is odd.  The total height of the quarry is related to the number of constant-diameter levels, 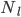by .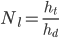

Given a 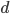and 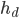, the total number of blocks you mine in a quarry, 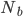, is found by simply adding up all the blocks at a given level and then adding all the levels.  Noting that 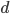decreases by two blocks each time you make the quarry square smaller,

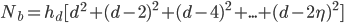
where 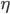is related to 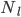.   Writing this in summation form,

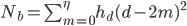
where 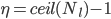.  Now, the summation bit is straightforward to see, but the upper limit 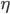took some playing around in Mathematica for me to work it out.  This seems to work pretty well, but if anyone can derive this limit (or a better one) more "rigorously", please let me know!