Two masses on a string going through a hole. Yeah, that's the stuff we learn about in physics class. Anyway, this is the first in a (possibly) series of posts where I work out some problem from my lecture notes or homework. The reason for doing this is because 1) there's a (small) chance it will be useful or interesting to someone else, and 2) the drawn out process of typing this up and thinking about how to explain it helps me study.
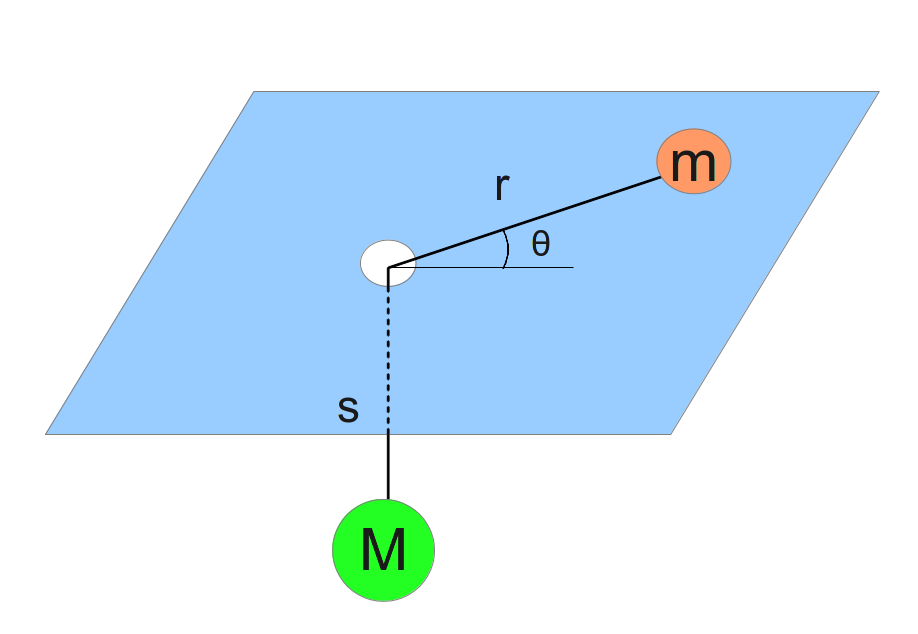
Figure 1, two masses on a string going through a hole.
Consider two masses connected by a string (figure 1). The ideal string passes through a hole in a plate which is parallel to the x-y plane. One mass, 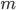 is sitting on the plate and is free to rotate about the hole with no friction. The second mass,
is sitting on the plate and is free to rotate about the hole with no friction. The second mass, 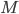 , is hanging below the plate and moves only in the vertical z direction under the influence of gravity. The total length of the string is
, is hanging below the plate and moves only in the vertical z direction under the influence of gravity. The total length of the string is  and we define
and we define 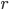 and
and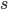 to be the distances between the hole and
to be the distances between the hole and 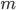 and
and 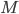 , respectively, so that
, respectively, so that 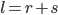 .
.
We can use Lagrangian mechanics to explore the system. In Cartesian coordinates, the total kinetic energy is the sum of the kinetic energy of each mass:
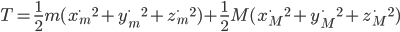 (1)
(1)
where we've used the dot notation for time derivatives.
Considering that  is only rotating about the
is only rotating about the  axis and
axis and 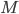 is moving only vertically, it makes sense to consider switching to a more reasonable coordinate system. We can transform to cylindrical coordinates with:
is moving only vertically, it makes sense to consider switching to a more reasonable coordinate system. We can transform to cylindrical coordinates with:
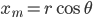
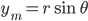
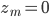
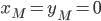
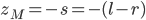
Taking derivatives of these with respect to time and inserting them into (1), we can rewrite the kinetic energy in cylindrical coordinates as
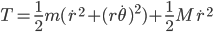
where 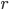 and
and 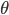 are now the generalized coordinates of the system. The potential energy depends only on the height of
are now the generalized coordinates of the system. The potential energy depends only on the height of 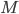 since
since 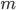 is confined to sit on the plate, so
is confined to sit on the plate, so
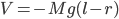
With 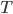 and
and 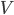 we can write the Lagrangian
we can write the Lagrangian 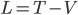 :
:
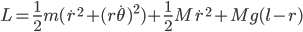
We see that 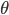 does not appear in the Lagrangian, which means that the generalized momentum corresponding to
does not appear in the Lagrangian, which means that the generalized momentum corresponding to 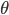 is a conserved quantity:
is a conserved quantity:
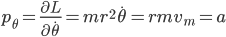 (2)
(2)
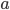 can be identified as the angular momentum of mass
can be identified as the angular momentum of mass 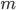 .
.
We can also look at the total energy 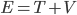 :
:
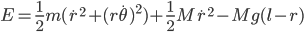 (3)
(3)
From (2) we see that 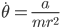 . Substituting this in (3) gives
. Substituting this in (3) gives
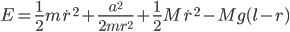
We can separate the constants on the left hand side and use the remaining terms to define an effective potential 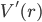 :
:
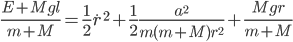
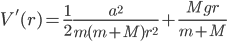
Imagine 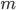 is rotating about the hole. This means there will be some centripetal (or centrifugal, depending on your reference system) acceleration which will pull the hanging mass
is rotating about the hole. This means there will be some centripetal (or centrifugal, depending on your reference system) acceleration which will pull the hanging mass 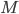 up. We want to find
up. We want to find 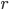 such that the force is an extremum. In other words:
such that the force is an extremum. In other words:
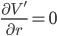
Setting the derivative equal to zero gives
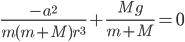
And solving for 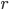 :
:
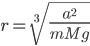
which gives the radius of "orbit" of mass 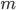 about the hole for a given angular momentum
about the hole for a given angular momentum 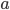 such that
such that 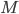 remains suspended in the air.
remains suspended in the air.


