I like this series of graphs because it looks like someone is pulling on the solution like it's a string, until SNAP! What's being shown here is the numerical solution to the initial value problem
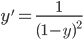 ,
, 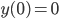 ,
, 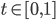 .
.
As you might suspect from the denominator, there's trouble when 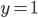 . This results in a problem that's not well-posed. Using the same numerical scheme but only a different number of grid points produces wildly different behaviors. What's basically happening is that if the numerical scheme hits the trouble region "just right" due to the grid point spacing, the gigantic derivative sends the solution flying off to some large and incorrect value.
. This results in a problem that's not well-posed. Using the same numerical scheme but only a different number of grid points produces wildly different behaviors. What's basically happening is that if the numerical scheme hits the trouble region "just right" due to the grid point spacing, the gigantic derivative sends the solution flying off to some large and incorrect value.
You can reproduce this figure in Mathematica with the following code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | (* 4th Order Runge-Kutta Method *) rungeKutta[y0_, npoints_, a_, b_, f_] := ( h = (b - a)/(npoints - 1); y = Table[0, {npoints}]; t = Table[0, {npoints}]; y[[1]] = y0; t[[1]] = a; Do[ yn = y[[n]]; tn = t[[n]]; m1 = f[tn, yn]; m2 = f[tn + 0.5*h, yn + 0.5*h*m1]; m3 = f[tn + 0.5*h, yn + 0.5*h*m2]; m4 = f[tn + h, yn + h*m3]; y[[n + 1]] = yn + (1/6)*h*(m1 + 2*m2 + 2*m3 + m4); t[[n + 1]] = tn + h; , {n, 1, npoints - 1}]; solution = Table[{t[[i]], y[[i]]}, {i, 1, Length[t]}]; Return[solution]; ); f[t_, y_] := 1/(y - 1)^2 y0 = 0; a = 0; (* Starting t *) b = 1; (* Ending t *) rks = {}; Do[ npoints = 10^5 + i; (* Number of grid points *) sol = rungeKutta[y0, npoints, a, b, f]; p = ListPlot[sol, PlotStyle -> {PointSize[0.001] , Orange}, Frame -> True, AxesLabel -> {"t", "y"}, PlotLabel -> "10^5+ " <> ToString[i] <> " grid points"]; AppendTo[rks, p]; , {i, 0, 4}]; GraphicsColumn[Table[rks[[j]], {j, 5}], Frame -> All, ImageSize -> 300] |
It'll probably take several seconds to run because of the large number of grid points used in each solution.
